A vespa é um inseto curioso. Não pelo fato de apenas as fêmeas terem o ferrão. Não por serem parasitas, nem pelo fato de que a grande parte dos insetos que hoje são considerados como pragas e são responsáveis pela fome no mundo tem uma vespa como predador natural.
As vespas podem ser dividades em espécies solitárias ou sociais. As solitárias constróem seus ninhos com lama, geralmente em lugares protegidos, como paredes, quinas de telhados, etc. Se você observar aqueles canudinhos de lama numa parede pode apostar que foi feita por uma vespa solitária. Mais do que isso, quando bota os ovos, a mamãe vespa o faz em células individuais, e prende em cada célula lagartas vivas que se tornarão o bigmac de seus bebês assim que estes sairem dos ovos.
Agora preste atenção, pois é aqui que a mágica acontece, fique de olho nos copos e tente adivinhar debaixo de qual a bolinha se encontra.
Algumas espécies de vespas SEMPRE deixam 5 lagartas em cada célula. Outras 12 e outras ainda 24 lagartas por célula. A vespa da espécie genus Eumenus colocará 5 lagartas na célula se o ovo for de um macho – que é menor – e 10 se for a célula futuramente ocupada por uma fêmea.
Se você parou para pensar como uma vespa sabe se vai sair um macho ou uma fêmea de um ovo; ou de onde é que ela arranja seu estoque de lagartas, mesmo quando não é época de lagartas; ou como é que ela monta uma estrutura de barro que consiga segurar 24 lagartas vivas se contorcendo sem partir, parabéns! Você errou feio o lugar onde a bolinha está.
Essa habilidade de contar e dividir – ou multiplicar, dependendo de que ponta você olha – da vespa é um traço inato dela, não tem a ver nem com condicionamento, nem com aprendizado. Ele faz parte do circuito básico das funções vitais dela.
Agora, vespas não possuem dedos, mas contam bem até 24 como vimos. Já seres humanos temos dedos, normalmente 5 em cada mão e 5 em cada pé – se não forem nativos de Goiânia, abençoados pelo Césio 137. Sendo assim nossa capacidade de contar deve dar da 1000 a zero sobre a de um inseto, certo? Ou ao menos de 20 a 6, já que eles tem 6 patas, certo?
É obvio que não!
Somos mamíferos, temos um cérebro evoluído, lidamos com noções abstratas o tempo todo, inventamos a física nuclear.
De forma geral uma pessoa comum tem uma capacidade básica numérica de contar até 4. Até os dias de hoje existem grupos de pessoas que não usam os dedos para contar e tem dificuldade de contar grupos com quatro ou mais elementos. Provavelmente isso não se refere a pessoas que puderam ir a uma escola para se tornar engenheiros ou traficantes que crack, mas tenha em mente que no mundo de hoje, essas pessoas, e você, fazem parte de uma minoria gritante da raça humana; Um grande número de seres humanos tem um sistema quantitativo próprio que distingue o 1, o 2 e o Muito, que incluiria o 3, o 4 e qualquer valor acima disso. Várias sociedades tribais ainda tem esse costume hoje. Mas o homem civilizado passa por um processo de condicionamento e então de aprendizado [1] que nos possibilita usar um pouco melhor esse senso numérico que temos. Crianças humanas, por exemplo, quanto atingem a idade aproximada de 14 meses, quase sempre são capazes de notar que algo está faltando dentro de um grupo com o qual ela esteja familiarizada [2]. Nesta mesma idade as crianças já conseguem montar objetos de um grupo que foram separados, mas sua capacidade de perceber diferenças numéricas em pessoas ou objetos ao seu redor se torna muito limitada quando o número vai além de 4. Salamandras quando condicionadas conseguem distinguir números que vão até o 16, que ainda é um número inferior ao 24 da vespa.
Vamos, vamos, não tem porque ficar triste por insetos contarem melhor do que você ou seus filhos. Afinal evolutivamente eles chegaram um pouco antes de nós na terra; dizem que os artrópodes surgiram aproximadamente a 570.000.000 de anos, já os primeiros insetos de fato surgiram a 400.000.000 de anos – curiosamente junto com as primeiras sementes – e só 2.400.000/2.300.000 é que nós começamos a engatinhar para longe das árvores. Os circuitos das vespas estiveram lidando com contagem muitos e muitos e muitos milhões de anos a mais do que nós.
Mas, diferente das vespas e de outros animais, nós fomos além. Não apenas nos condicionamos a lidar com quantidades numéricas mais complexas como também desenvolvemos um processo de aprendizado que nos permitiu ir além da mera contagem e simples aritmética.
Para continuarmos com essa discussão unilateral vamos ter que fazer uma pausa para entrar no mundo da metafísica. Já vimos que muito tempo atrás o ser humano se envolveu com religião. De uma forma ou outra isso é uma abstração que vai além da simples abstração. A noção de tempo, por exemplo, é uma abstração por si só complicada, não apenas perceber o ciclo das coisas, mas dividir esse ciclo em partes menores e administráveis. Agora a religião lida com algo diferente. O tempo é algo impessoal. A religião trata com algo que tem uma vontade, com um algo abstrato com o qual podemos lidar e interagir, pedir e xingar. Ofereça um gamo para uma hora e ela continuará sendo uma hora. Ofereça um gamo para o Deus Caçador e você está garantindo que os gamos continuarão surgindo para que você não morra nem de fome nem de frio. Essa facilidade para a abstração talvez tenha sido responsável por outra ainda maior do que um simples conceito de horas, da atropomorfisação de constelações ou de Deuses ou Deusas, a abstração de números.
No grande clássico dos anos 1980, O Massacre da Serra Elétrica Parte II, existe um diálogo muito esclarecedor sobre alguns aspectos básicos, porém importantes, da vida. A família Sawyer está reunida no parque de diversões do diabo quando percebem que Bubba, também conhecido como Leatherface, não matou a Dj Stretch, Chop Top começa a cantar:
– Bubba tem uma namorada, bubba tem uma namorada!
Drayton Sawyer então chega junto de Leatherface e diz:
– Você tem uma escolha, rapaz: sexo ou a serra. Sexo é, bem… ninguém sabe. Mas a serra, a serra é a família.
Linda cena, meus olhos se enchem de lágrimas apenas de relembrar. Bem, vamos adaptar isso para nossa realidade imediata.
“Números são, bem… ninguém sabe.”
Números surgiram como a necessidade de dar nome a algo que ninguém sabe direito o que é. Pense em uma maçã. Onde está o número?
a) 1 maçã
b) 300 gramas
c) 1 macieira
d) Todas as anteriores
e) Nenhuma das anteriores
O número varia em relação a um mesmo objeto de acordo com a nossa atenção e de acordo com o interesse de nosso foco. Números são coisas mais sinistras do que deuses. Deuses ainda podem ter um comportamento imprevisível, mas mesmo assim é algo que conseguimos ver como funciona; agora pense, se todo número elevado a 0 é igual a 1, e 0 elevado a qualquer número é 0, quanto é 0 elevado a 0? Esqueça aquela conversa de Deus criar uma pedra tão grande que até Ele não consiga erguer. Números são piores.
Nosso pai dos burros afirma que um número é a “relação entre uma quantidade e outra quantidade, tomada como termo de comparação e chamada unidade.” Uhmmmm isso é merda. E vou mostrar o porque agora. Imagine uma imagem de Nossa Senhora pelada. Em seguida imagine a imagem de um selo postal.
Como foi que você olhou para ela? Seu cérebro beteu uma foto do todo e você reparou em tudo ao mesmo tempo ou seus olhos foram pulando de detalhe em detalhe? Nossa, peitos! Meu Deus, é Maria? Nossa, Maria era depilada? Mas é mesmo ela? Olhe de novo, se quiser clicar na imagem para ver ela maior e mais viril, fique à vontade. Se você é um ser humano normal, com um sistema nervoso padrão de fábrica, você “escaneou” várias partes da imagem e foi compondo o todo na mente. Agora se você é MESMO um ser humano, e não um repolho, por exemplo, você fez esse escaneamento de forma aleatória sobre a superfície, não começou olhando no canto superior esquerdo e foi olhando linha por linha até em baixo.
A coisa fica assustadora quando passamos para a imagem logo abaixo da primeira. Ela é um selo. Mais precisamente um Treskilling Yellow. Independente deste selo impresso em 1857 ter sido vendido por mais dinheiro do que você jamais vai ver de uma só vez em sua vida[**] ele é uma imagem relativamente menor e com menos detalhes do que o quadro acima. Apesar de ser menor, ter menos detalhes e parecer muito mais sem graça, o seu processo de observação foi o mesmo. Sua atenção se concentra em pequenas partes aleatórias da imagem do selo e então você monta a imagem na sua mente.
E isso não é porque as duas tem detalhes ou palavras ou precisam fazer sentido. A sua mente executa o mesmo processo para observar um feijão. Duvida? Olha o feijão abaixo. Me diga, ou melhor, se diga se bateu o olho e já viu a imagem toda ou se seus olhos zanzaram de um lado para o outro montando ela?

Não importa o tamanho, detalhe ou complexidade do que olhamos, nossos olhos saem como loucos pulando de um lado para outro, dentro da área que contém aquilo que está sendo observado e a partir de suas partes isoladas vai construindo a figura, seria seguro dizer que mesmo no caso do feijão, você para de prestar atenção logo após um primeiro olhar de relance porque assim que junta alguns poucos dados aleatórios sobre ele já puxa a imagem mental “feijão” de seu arquivo platônico e julga que não precisa perder mais tempo reparando em cada detalhe de sua área. Para não ficar repetindo que isso ocorre de forma aleatória vamos dar nomes aos bois. Aquele é Arnaldo, aquele Jonas Jr, e este que discutimos se chama fractal. Nossos olhos percebem o mundo através de um padrão fractal de movimento, e através desse padrão eles montam as imagens do que vemos. Como nosso cérebro foi programado para poupar tempo e economizar energia, nós não precisamos nos deter em cada milímetro do que estamos observando para perceber o que é o objeto e então encerrar a observação. Não fomos criados para observar algo todo de uma vez ou então olhando em uma ponta e deslizando a visão calmamente para a outra criar a imagem como um scaner, assim como também não fomos criados para analisar cada micro irregularidade de uma forma, apenas o padrão geral e determinar a que grupo aquilo se encaixa. Nossa cabeça é uma zona, e nossa capacidade de observar o mundo não poderia ser diferente. Assim, quando você olha pela janela ou quando tenta ver a sujeira debaixo da unha, está esquadrinhando a área observada seguindo um padrão aleatório fractal para conseguir entender aquilo que os olhos mostram, e termina a observação assim que tem a quantidade mínima necessaria de informação para se criar um padrão.
Colocando o parágrafo acima em uma línguagem mais simples, cada vez que você olha para uma coisa, está iniciando uma brincadeira de Onde Está Wally [4], a diferença é que não está procurando um detalhe em especial, apenas tentando entender o que é a massa disforme para a qual está olhando para então lhe dar uma forma.
Pausa
Fim da pausa
Ufa.
Bem, se nossa mente não consegue trabalhar com um conceito de unidade visual, ou seja, um quadro, um selo, um feijão. Então como esperar que nosso cérebro trabalhe com esse mesmo conceito: “Isto é uma unidade!”
NÃO EXISTEM UNIDADES NA NATUREZA!!!
Os gregos já falavam de átomos, apenas para milênios depois descobrirem que átomos, os indivisíveis, era feitos por partes menores, então cada parte menor era feita por partes menores, e assim até chegarmos em algo que não pode ser mais compreendido como matéria, partícula ou nada assim. Simplesmente existe, mas desaparece.
Como então supor que números sirvam para representar uma unidade?
E se um número é uma relação entre uma unidade e outra unidade, assim que o primeiro macaco resolveu trocar bananas por alguma outra coisa, essa noção foi por ralo a baixo. Suponha que você planta batatas, e está cansado de batatas, você quer uma companheira. Então leva um saco de batatas para a aldeia vizinha, onde se criam cabras, e vai negociar. 1 cabra = 50 batatas, na promoção saem 2 cabras por 70 batatas. Na troca existe um padrão de “as batatas tem que pesar pelo menos tanto, ou ter tal tamanho” ou será que você podia ser malaco e levar apenas batatas pequenas? Da mesma forma, será que a cabra, ou cabras, seriam cabras suecas, versadas nas mais loucas artes de amor, ou seriam as cabras largadas que não produzem todo o leite que o dono delas gostaria que produzissem?
Qualquer começo de argumento nas linhas: “é por isso que se criaram regras de peso e medida” já começou errado.
O ser humano sempre procurou proporcionalidade, não para si, é claro, mas para os outros. Afinal se eu posso dar uma batata e voltar com cinco cabras para casa, ótimo para mim, mas se tenho que dar sete anos de colheita farta para conseguir dar uma ordenhadinha… nem fodendo!
Em 1901, um bando de franceses encontrou na mesopotâmia, mais precisamente no que hoje chamamos de Irã, um monolito preto com 2,25m metros de altura, mais fino na ponta do que na base, inscrito com 282 leis e um desenho do topo.

Se isso não é o maior dildo jamais descoberto no mundo eu não sei o que é. Os especialistas, cheios de pudor, ao invés de olhar qual o objetivo mais óbvio deste objeto resolveram se focar – seguindo um padrão fractal de observação – no que havia rabiscado ali. Depois de um tempo declararam que aquilo era um dos mais antigos conjuntos de leis escritas já encontrados, datado de 1700 a.C. e supostamente elaborado pelo rei Hamurabi. Esse código dividia a sociedade em três classes e destilava não apenas regras para uma vivência harmoniosa, mas também a punição para quem não seguisse as regras. Resumindo todo o texto existente no monolito Hamurabi declara, no epílogo que criou aquelas leis “para que o forte não prejudique o mais fraco, a fim de proteger as viúvas e os órfãos” e “para resolver todas as disputas e sanar quaisquer ofensas”. Quando olhamos para algumas das leis e penitências como por exemplo:
Art. 25 § 227 – “Se um construtor edificou uma casa para um Awilum, mas não reforçou seu trabalho, e a casa que construiu caiu e causou a morte do dono da casa, esse construtor será morto”.
e
§ 230 – “Se uma casa mal-construída causa a morte de um filho do dono da casa, então o filho do construtor será condenado à morte”.
Já vemos que por “evitar que um prejudique o outro e evitar ofensas dando bicotas em viúvas”, o código de leis buscava justamente a proporcionalidade. O famoso olho por olho dente por dente. E não existe a necessidade numérica para isso.
Assim, a idéia de que números tem a ver com proporcionalidade não está inteiramente correta. A vida em sociedade necessita, com ou sem matemática, de uma proporção. Se você pisa no meu pé eu tecnicamente não posso estuprar seus pais e matar seus filhos, por mais que eu tenha vontade, pois a minha resposta seria desproporcional à ofensa que você me cometeu.
Também quando falamos em comparar, não estamos falando de comparar qualidades intrinsecas de cada objeto. Se fôssemos parar para analisar um carro e ver o quanto ele vale, perderíamos um dia inteiro para ver cada pedaço dele e tirar da tabela do carro ideal aquilo que falta ou está danificado ou foi modificado para chegar a um valor – equivalente monetário dele. Por isso geralmente criamos um padrão médio do que vale um carro padrão e corremos o risco de pagar a mais ou a menos para não ter o trabalho de avaliar cada centímetro quadrado dele. O mesmo vale para qualquer coisa onde vá existir uma troca. Qualquer pessoa ajuizada sabe qua qualquer sistema de pesagem ou medição é falho, quanto mais rudimentar mais falho, e quando as pessoas começaram a negociar para uma coisa ser rudimentar ela tinha que ser muito, mas muito desenvolvida, nos padrões que temos hoje, e mesmo hoje nossas medições são estupidamente imperfeitas.
Se não temos como estabelecer o que é unidade, não temos meios reais de fato de falar em comparações e a relação entre quantidades tem mais a ver com a necessidade do que a uma qualidade intrinseca do que está sento quantitativado (o que você daria por um remédio que pode curar a leocemia de uma pessoa que você ama, e quanto daria por um remédio que pode curar a leocemia se você não conhece ninguém que sofre disso?), então o que nos resta sobre os números?
Curiosamente existe a história de um corvo que incomodava muita gente.
Um corvo construiu seu ninho na torre da residência de um agricultor. Incomodado com aquela situação o agricultor decide matá-lo. O corvo percebendo a presença de alguém saia da torre.
Então o agricultor usou da seguinte estratégia: duas pessoas entraram na residência e uma saiu, ficando a outra lá dentro e mesmo assim o corvo não retornou, pois percebeu que havia uma pessoa lá dentro. O procedimento foi repetido com três pessoas, ficando uma e saindo duas, com quatro, ficando uma e saindo três e o corvo não retornava, pois percebia que havia uma lá dentro.
Quando entraram cinco pessoas e saíram quatro, então o corvo retornou ao seu ninho e foi morto pelo agricultor por causa da sua percepção de contar até quatro.
Que lição podemos tirar deste conto, e dos outros exemplo contidos aqui?
- Nosso sistema neurológico de contagem chega num ponto em que não distingue muitos de 4, por exemplo; e isso se não o envenenarmos antes.
- Números, operações matemáticas e conjuntos não precisam ser aprendidos, nós viemos com eles como bônus de fábrica;
- A capacidade de contar pode estar muito mais relacionada a nossa capacidade de sobreviver do que imaginamos (eu não entro naquela caverna enquanto os 5 tigres que entraram não saírem);
- A abstração matemática não requer uma sofisticaçnao evolutiva grande. Os homens das cavernas brincavam com números primos já.
- A passagem dos números do universo abstrato para o concreto deve ter tido alguma ligação com o desenvolvimento da linguagem.
Isso pode soar como loucura, ou um chute completamente aleatório sobre o assunto, mas não tira a verdade da suposição. Um número na sua cabeça está preso e não possui comparação aos números na cabeça do macaco sentado na minha frente no metrô, assim como saber se o meu 3 é igual ao três dele? Uma vez que a linguagem se desenvolve e se estabelece como forma preferida de comunicação, no lugar da arte ou da telepatia, começamos a empurrar nossos símbolos goela abaixo dos outros que convivem com a gente e começamos a trabalhar com uma média, estabelecendo não mais significados pessoais, mas universais para algo, com isso definindo grupos padrões aos quais conceitos podem ser aplicados. Assim não existe uma batata padrão que possa ser usada de base para se trocar por uma pêra, e sim cria-se um grupo batata que possui uma média que pode ser relacionada, artificialmente com a média pêra criada.
Um exemplo claro disso é o exercício proposto logo abaixo.
EXERCÍCIO PROPOSTO LOGO ABAIXO
Pegue uma folha de papel e desenhe três fileiras de três pontos, ou se preferir três colunas de três pontos, como esta abaixo. Se tiver dificuldades para isso, aproveite quando ninguém estiver olhando, coloque uma folha em cima do monitor e use o meu desenho de cola e faça o seu rapidinho:

Agora, seu objetivo traçar quatro retas que toquem todos os pontos.
Regras:
Toda reta deve ser reta, nada de retas curvas.
Uma reta deve obrigatoriamente ter início onde a última terminou.
As retas podem se cruzar quantas vezes você quiser. Pode passar mais de uma reta por um mesmo ponto.
Você pode fazer o exercício sem as roupas se quiser.
As quatro devem passar por cima de todos os pontos em cheio, não de ladinho, não de quininha e nem raspando.
Se não entendeu eu vou desenhar para você:
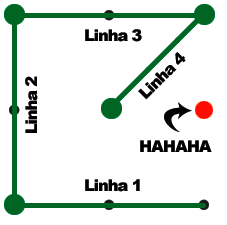
É claro que no exemplo falta um ponto. Mas você é livre para usar sua intuição de macaco para se safar dessa, a resposta é simples, as regras são simples. Pense numa vespa capaz de dividir e multiplicar e mãos à obra.
Notas:
[1] Abracadabra
[2] Pintinhos, como vimos aqui, conseguem distinguir isso muito mais cedo na vida.
[3] O selo postal mais caro do mundo, o sueco “Treskilling Yellow”, foi vendido neste sábado (22) em Genebra a um consórcio internacional que não revelou sua identidade nem o montante da transação.
“Os integrantes do consórcio fizeram a compra considerando que se trata de um sólido investimento em tempos de crise”, destaca a casa de leilões David Feldman, precisando que o selo é o mais caro do mundo.
O selo já havia sido vendido em 1984, 1990 e 1996, quando chegou ao preço de 2,875 milhões de francos suíços (3,61 milhões de euros).
O “Treskilling Yellow” da Suécia foi descoberto por acaso, em 1885, por um jovem sueco de 14 anos que descolava selos de um velho álbum para tentar revendê-los, esperando engrossar um pouco sua mesada. O sueco Treskilling – habitualmente verde – foi impresso por erro em 1857.
Pertenceu a diferentes colecionadores, assim como a um aristocrata alemão que vivia na França e a um magnata belga.
[4] Onde Está Wally? é uma série de livros ilustrados de caráter infanto-juvenil criada pelo ilustrador britânico Martin Handford. No livro o leitor encontra ilustrações que ocupam duas páginas inteiras, nas quais em algum lugar está desenhado Wally, personagem central da série, e alguns de seus objetos. Wally sempre veste-se com uma camisa listrada em vermelho e branco, e com um gorro de mesmas cores. Também possui uma bengala e usa óculos. Ele geralmente perde seus pertences, como livros, equipamentos de acampamento ou seus sapatos, e o seu objetivo é encontrá-los.
Caso esteja sentindo que o tédio no escritório o domina, largue tudo por um objetivo mais nobre e realize um estudo sobre os padrões fractais dos olhos ao tentar observar uma imagem aqui – lembre-se, você está fazendo isso em noma da ciência.
Por LöN Plo
Postagem original feita no https://mortesubita.net/mindfuckmatica/a-natureza-pervertida-dos-numeros/

[…] Postagem original feita no https://mortesubita.net/mindfuckmatica/a-natureza-pervertida-dos-numeros/ […]